2D坐标系与3D坐标系的相互转换--python实现

发表于   |   分类于   |  

并不是做关于SLAM方向的，但由于某些任务涉及到，故作此笔记～

相机内参矩阵：
不同的的深度摄像头具有不同的特征参数，在计算机视觉里，将这组参数设置为相机的内参矩阵C:
$$\begin{bmatrix} f_x& 0 &c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}$$

fx，fy指相机在x轴和y轴上的焦距，cx，cy是相机的光圈中心，这组参数是摄像头生产制作之后就固定的。

世界坐标系: 用户定义的三维师姐坐标系，以某个点为远点，为描述目标物在真实师姐里的位置而被引入

相机坐标系: 以相机为原点建立的坐标系，为了从相机的角度描述物体的位置而定义，作为沟通世界坐标系和图像/像素坐标系的中间一环。

学习自: 三维坐标变换——旋转矩阵与旋转向量

旋转矩阵:

使用矩阵来表示一个旋转关系有两个缺点： 1）通过旋转矩阵不能直观地看出旋转的方向和角度 2）另一方面：旋转变换有3个自由度，旋转矩阵中的元素不是相互独立的。

旋转向量:
设旋转向量的单位向量为r，模为θ。三维点（或者说三维向量）p在旋转向量 r 的作用下变换至 p′，则：
$$p’=\cos\theta\cdot p+(1-\cos\theta)(p\cdot r)r+\sin\theta\cdot r \times$$ p

学习自:计算机视觉：相机成像原理：世界坐标系、相机坐标系、图像坐标系、像素坐标系之间的转换

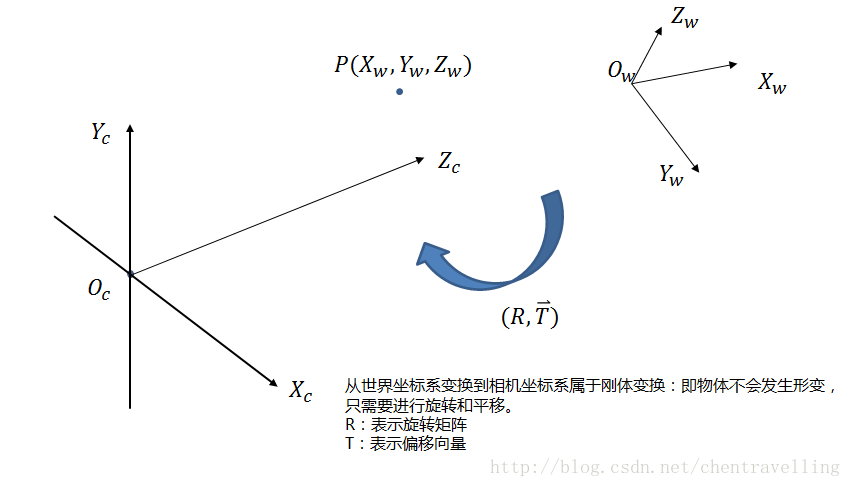
从世界坐标系到相机坐标系: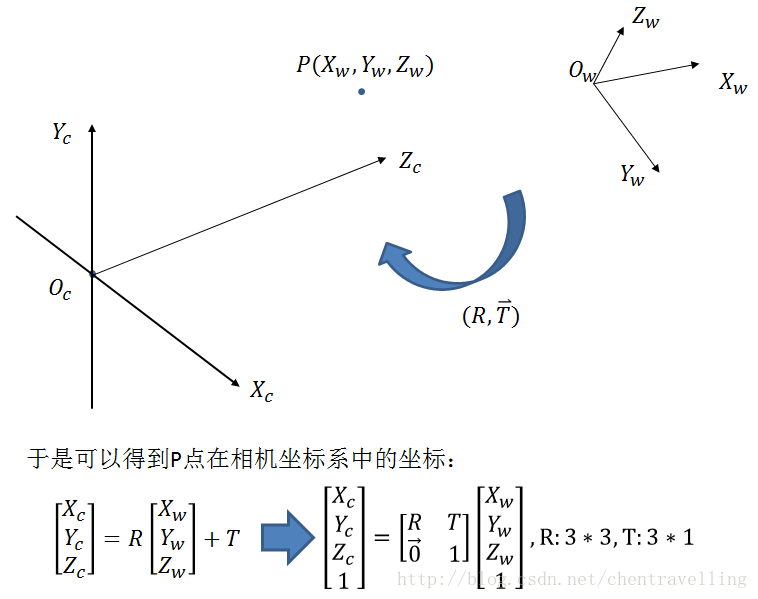

相机坐标系与图像坐标系: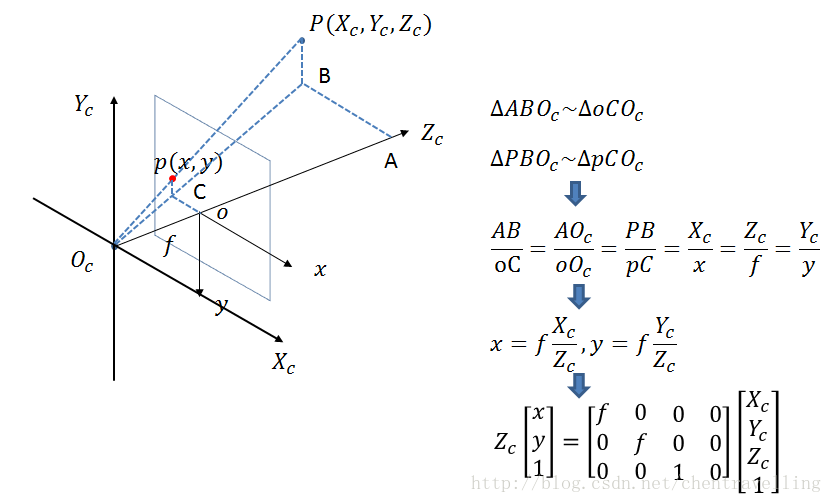

图像坐标系与像素坐标系:

像素坐标系和图像坐标系都在成像平面，只是各自的原点和度量单位不大一样，图像坐标系的原点为相机光轴与成像平面的交点。图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel

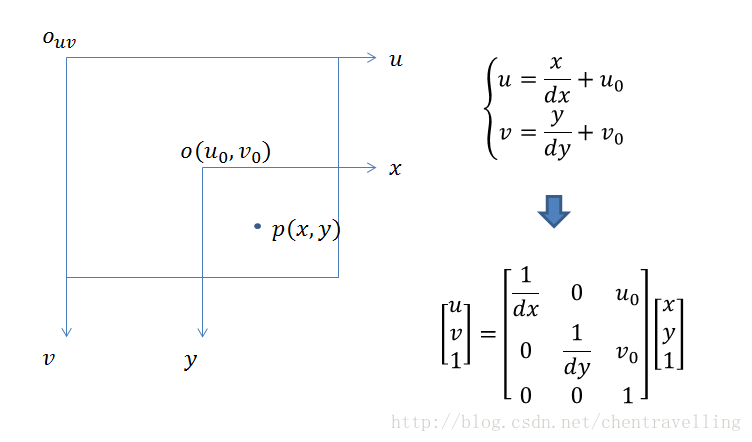
像素坐标系与世界坐标系: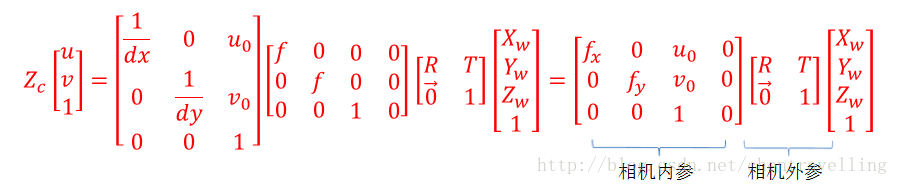

convert2Dto3D

通过上面的公式，将像素坐标系的点映射到世界坐标系上，由于二维坐标映射到三维坐标会多了一个深度信息，因此二维点映射到三维坐标系，得到的是一条射线。虽然通过下面的代码得到的确实是一个三维的坐标点，但是其实是不确定的，与光点连线上（射线）所有的点都满足条件

convert3Dto2D

将3D平面的box转成2D平面的box，通过cv.projectPoint(三维平面下的8个点，旋转矩阵， 平移向量， 相机内参， 0)可以得到3D平面下的8个点映射到2维平面下8个点的坐标

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

# 此函数只是外部定义而已，大家可自行定义
camera_matrix, rvec, tvec = camera_params()

print("相机内参:", camera_matrix)

print("平移向量:", tvec)

print("旋转矩阵:", rvec)

# (R T, 0 1)矩阵
Trans = np.hstack((rvec, [[tvec[0]], [tvec[1]], [tvec[2]]]))

# 相机内参和相机外参 矩阵相乘
temp = np.dot(camera_matrix, Trans)

Pp = np.linalg.pinv(temp)

# 点（u, v, 1) 对应代码里的 [605,341,1]
p1 = np.array([605, 341, 1], np.float)

print("像素坐标系的点:", p1)


X = np.dot(Pp, p1)

print("X:", X)

# 与Zc相除 得到世界坐标系的某一个点
X1 = np.array(X[:3], np.float)/X[3]

print("X1:", X1)


## 3D 转成 2D
from utils import *
import numpy as np
import cv2

## 2D 转成 3D

# 此函数只是外部定义而已，大家可自行定义
camera_matrix, rvec, tvec = camera_params()

print("相机内参:", camera_matrix)

print("平移向量:", tvec)

print("旋转矩阵:", rvec)

# (R T, 0 1)矩阵
Trans = np.hstack((rvec, [[tvec[0]], [tvec[1]], [tvec[2]]]))

# 相机内参和相机外参 矩阵相乘
temp = np.dot(camera_matrix, Trans)

Pp = np.linalg.pinv(temp)

# 点（u, v, 1) 对应代码里的 [605,341,1]
p1 = np.array([605, 341, 1], np.float)

print("像素坐标系的点:", p1)


X = np.dot(Pp, p1)

print("X:", X)

# 与Zc相除 得到世界坐标系的某一个点
X1 = np.array(X[:3], np.float)/X[3]

print("X1:", X1)


## 3D 转成 2D
## cube为世界坐标系的8个点的三维坐标
cube = np.float64([[-3.102,-1.58400011, 9.29399872],[-3.102, -0.08400005, 9.29399872]
 ,[-1.27200007,-0.08400005 , 9.29399872]
 ,[-1.27200007, -1.58400011  ,9.29399872]
 ,[-3.102   ,   -1.58400011 ,13.8939991 ]
 ,[-3.102   ,   -0.08400005, 13.8939991 ]
 ,[-1.27200007 ,-0.08400005, 13.8939991 ]
 ,[-1.27200007, -1.58400011 ,13.8939991 ]])
result, _ = cv2.projectPoints(cube, rvec, tvec, camera_matrix, 0)
print("3D to 2D 的 8个点的坐标：", result)